1. Python Tutorial
  2. Python Numpy
  3. Multinomial Distribution in Python

Multinomial Distribution in Python

Submitted by moazkhan on Wednesday, July 1, 2020 - 22:23.

In this tutorial you will learn:

  • What is Multinomial Distribution?
  • Multinomial Distribution Implementation in python
  • Visualization of Multinomial Distribution

Multinomial Distribution

Multinomial Distribution is a probability distribution which is used to calculate the distributions of experiments involving two or more variables/ outcomes. Binomial Distribution is a type of Multinomial Distribution with only two outcomes for example head/ tail and true/ false. In Multinomial Distribution multiple repeated trials are carried out with equal probability of each outcome and with each trial producing a specific outcome, as an example the outcome of tossing a coin can be head or tail.

Multinomial Distribution in Python

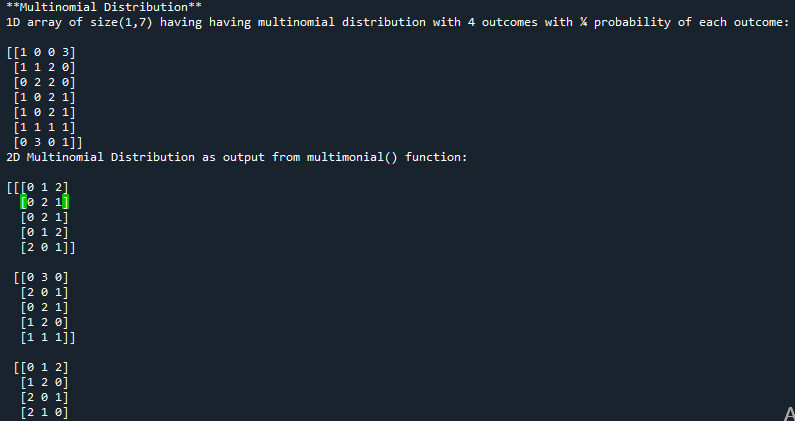
Multinomial distribution in python is implemented using an inbuilt function multinomial() which is included in the random module of NumPy library. The multinomial() function takes in two mandatory parameters and one optional parameters. First parameter “size” is the mandatory parameter and it is size of the output array which could be 1D, 2D, 3D or n-dimensional (depending on the programmer’s requirements). The second parameter is the number of possible outcomes defined by “n”. Third parameter “pvals”, it is the list of probabilities of outcomes and it is a 1D array of size (1, n). Lets take an example, we will generate a 1D array(1,7) of multinomial distribution with 4 outcomes, with each outcome with the probability of 0.25.
  1. #importing the random module
  2. from numpy import random
  3. #applying the multinomial function with 4 outcomes, with probability 0.25 of each outcome
  4. res_arr= random.multinomial(n=4, pvals=[1/4,1/4,1/4,1/4], size=7)
  5. #printing the results
  6. print('1D array of size(1,7) having having multinomial distribution with 4 outcomes with ¼ probability of each outcome:\n')
  7. print(res_arr)
In this example we will generate a 2D array of multinomial distribution having size (3,5), in the first line of code we are importing random module from numpy library and in third line we are calling the multinomial function with 3 outcomes, with probability of each outcome equal to 1/3
  1. #importing the random module
  2. from numpy import random
  3. #here we are using multinomial function to generate multinomial distribution of size 3 x 5 with 3 outcome with probability 1/3 of each outcome
  4. res_arr = random.multinomial (n = 3, pvals=[1/3,1/3,1/3], size=(3,5))
  5. print('2D Multinomial Distribution as output from multimonial() function:\n')
  6. #printing the result
  7. print(res_arr)
Lets take another example, in this example we will generate a 3D array of multinomial distribution of the size(3,3,5) with 8 possible outcomes with probability of 0.125 each
  1. #importing the random module
  2. from numpy import random
  3. #here we are using logistic function to generate logistic distribution of size 3 x 3 x 5
  4. res = random.multinomial(size=(3,3,5), n = 8, pvals=[1/8,1/8,1/8,1/8,1/8,1/8,1/8,1/8])
  5. print('3D Multinomial Distribution as output from multinomial() function:\n')
  6. #printing the result
  7. print(res)

Visualization of Multinomial Distribution

In this example we will visualize the Multinomial Distribution with 3 outcomes, with 1/3 probability of each outcome. Here we can observe that the plotted graphs has three peaks which directly correspond with the number of outcomes.
  1. #importing all the required modules and packages
  2. from numpy import random
  3. import matplotlib.pyplot as mpl
  4. import seaborn as sb
  5. #here we are using multinomial function to generate distributions of size 1000 with 3 outcomes each having probability 1/3
  6. sb.distplot(random.multinomial(size=1000,n=3,pvals=[1/3,1/3,1/3]), hist=False, label='normal')
  7. #plotting the graph
  8. mpl.show()

Add new comment

About text formats
  • 493 views