Trees in C++
Submitted by moazkhan on Sunday, August 24, 2014 - 11:15.
Trees in C++
Now, we know the basics of efficiency analysis and if I find some space in tutorial, efficiency calculation will be discussed but mean while, it is very important to cover other important data structures. Some images will be used to explain properly.
In this tutorial, you will learn
1. Concept of trees
2. Concept of binary trees (Most important tree)
3. Concept of binary search trees
4. How to make a class of node of binary search trees
What are trees in programming?
I will try not to use very technical language and try to explain it in the simplest way possible. In trees, we have a parent node from which daughter nodes originate. Each daughter node has just one parent but a parent can have any number of daughters (can be fixed for some type of trees like in binary trees, every parent has two daughters ). I realize it would still be unclear so I would use an image.
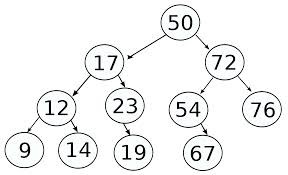 Here, every number which is encircled is a node. The node at the top is called root. From every root, a branch originates. This means that the line connecting 50 and 17 is a branch. Now, the node higher in the tree is called parent where as the node lower in tree is called child or daughter node. E.g. 50 is the parent of 17 and 72. Now, the node at the bottom is called leaf. Technically, leaf is a node which has no children. You can see that the number of parent of each node is one but the number of children is not specified.
Trees are non linear data structures. It means that there are several ways to go from a single node. If a tree has no node then it is called null or empty tree. It should be noted in a tree, there are also sub trees. 50 (root node) has a right sub tree( 72 as root node ) and a left sub tree( 17 as root node).
What is a binary tree?
A binary tree is a tree where each node has at most 2 children. These children are named as left child and right child. In a binary tree may have even a single child or no child at all but the maximum number of children are fixed which are two. There are types of binary search trees and they will be discussed in detail.
What is a binary search tree?
A binary search tree is a type of binary tree with the following condition.
If there is a node having value x then its left child should have value less than x and right child should have value greater than x.
It means that if a node has value 17 and it has 2 children 22 and 15. 15 will be left child and 22 will be right child. If the node “17” has children 22 and 23, then it will have no left child and both will be adjusted on right.
Here, every number which is encircled is a node. The node at the top is called root. From every root, a branch originates. This means that the line connecting 50 and 17 is a branch. Now, the node higher in the tree is called parent where as the node lower in tree is called child or daughter node. E.g. 50 is the parent of 17 and 72. Now, the node at the bottom is called leaf. Technically, leaf is a node which has no children. You can see that the number of parent of each node is one but the number of children is not specified.
Trees are non linear data structures. It means that there are several ways to go from a single node. If a tree has no node then it is called null or empty tree. It should be noted in a tree, there are also sub trees. 50 (root node) has a right sub tree( 72 as root node ) and a left sub tree( 17 as root node).
What is a binary tree?
A binary tree is a tree where each node has at most 2 children. These children are named as left child and right child. In a binary tree may have even a single child or no child at all but the maximum number of children are fixed which are two. There are types of binary search trees and they will be discussed in detail.
What is a binary search tree?
A binary search tree is a type of binary tree with the following condition.
If there is a node having value x then its left child should have value less than x and right child should have value greater than x.
It means that if a node has value 17 and it has 2 children 22 and 15. 15 will be left child and 22 will be right child. If the node “17” has children 22 and 23, then it will have no left child and both will be adjusted on right.
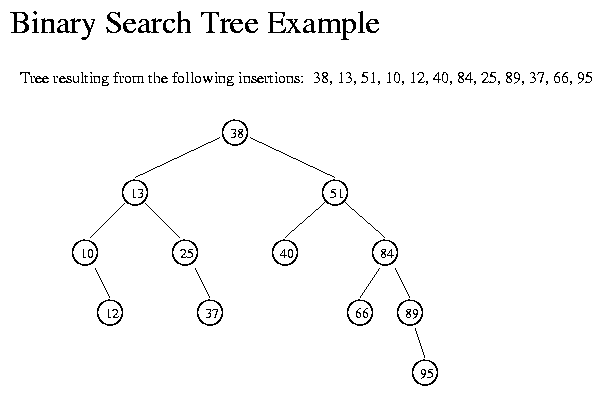 Here, we can see that all nodes to the left of 38 are less than 38 and all nodes to the right of 38 are greater than 38. Similarly, the same logic holds for all the sub trees. E.g. 13 has two children 10 and 25. 10 is on left of 13 and 25 is on right of 13. Even though, 12 is not directly attached to 13 but it is on left side of 13 because it is less than 13.
How do we make the class of a node of a Binary Search Tree?
Given below is the C++ code of binary search tree.
As a binary search tree can have maximum of two nodes so we have to make two pointers. Each pointer points to either left child or right child. In the constructor, left and right are given value equal to NULL. This is due to several reasons.
1. If it is NULL we know for sure that this node has no children. We can calculate number of children this way.
2. If it is not given value equal to NULL, it will cause problems during traversal. If we reach one of these pointers and it points to random address then it can create problems for us.
3. It is used in some other functions besides traversal.
Note: We will hopefully discuss implementation of binary search trees in next tutorial.
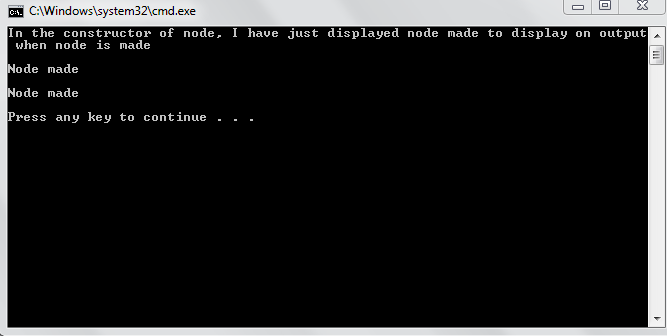
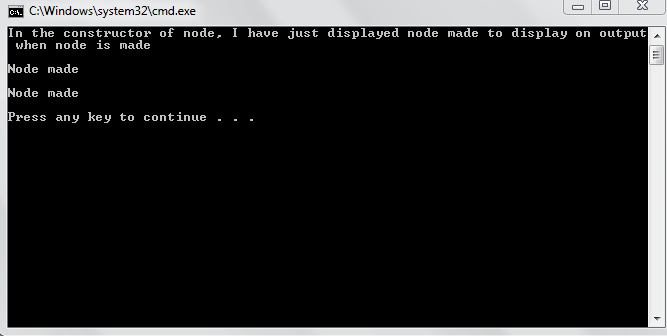
Output:
Here, we can see that all nodes to the left of 38 are less than 38 and all nodes to the right of 38 are greater than 38. Similarly, the same logic holds for all the sub trees. E.g. 13 has two children 10 and 25. 10 is on left of 13 and 25 is on right of 13. Even though, 12 is not directly attached to 13 but it is on left side of 13 because it is less than 13.
How do we make the class of a node of a Binary Search Tree?
Given below is the C++ code of binary search tree.
As a binary search tree can have maximum of two nodes so we have to make two pointers. Each pointer points to either left child or right child. In the constructor, left and right are given value equal to NULL. This is due to several reasons.
1. If it is NULL we know for sure that this node has no children. We can calculate number of children this way.
2. If it is not given value equal to NULL, it will cause problems during traversal. If we reach one of these pointers and it points to random address then it can create problems for us.
3. It is used in some other functions besides traversal.
Note: We will hopefully discuss implementation of binary search trees in next tutorial.
Output:
 Here, every number which is encircled is a node. The node at the top is called root. From every root, a branch originates. This means that the line connecting 50 and 17 is a branch. Now, the node higher in the tree is called parent where as the node lower in tree is called child or daughter node. E.g. 50 is the parent of 17 and 72. Now, the node at the bottom is called leaf. Technically, leaf is a node which has no children. You can see that the number of parent of each node is one but the number of children is not specified.
Trees are non linear data structures. It means that there are several ways to go from a single node. If a tree has no node then it is called null or empty tree. It should be noted in a tree, there are also sub trees. 50 (root node) has a right sub tree( 72 as root node ) and a left sub tree( 17 as root node).
What is a binary tree?
A binary tree is a tree where each node has at most 2 children. These children are named as left child and right child. In a binary tree may have even a single child or no child at all but the maximum number of children are fixed which are two. There are types of binary search trees and they will be discussed in detail.
What is a binary search tree?
A binary search tree is a type of binary tree with the following condition.
If there is a node having value x then its left child should have value less than x and right child should have value greater than x.
It means that if a node has value 17 and it has 2 children 22 and 15. 15 will be left child and 22 will be right child. If the node “17” has children 22 and 23, then it will have no left child and both will be adjusted on right.
Here, every number which is encircled is a node. The node at the top is called root. From every root, a branch originates. This means that the line connecting 50 and 17 is a branch. Now, the node higher in the tree is called parent where as the node lower in tree is called child or daughter node. E.g. 50 is the parent of 17 and 72. Now, the node at the bottom is called leaf. Technically, leaf is a node which has no children. You can see that the number of parent of each node is one but the number of children is not specified.
Trees are non linear data structures. It means that there are several ways to go from a single node. If a tree has no node then it is called null or empty tree. It should be noted in a tree, there are also sub trees. 50 (root node) has a right sub tree( 72 as root node ) and a left sub tree( 17 as root node).
What is a binary tree?
A binary tree is a tree where each node has at most 2 children. These children are named as left child and right child. In a binary tree may have even a single child or no child at all but the maximum number of children are fixed which are two. There are types of binary search trees and they will be discussed in detail.
What is a binary search tree?
A binary search tree is a type of binary tree with the following condition.
If there is a node having value x then its left child should have value less than x and right child should have value greater than x.
It means that if a node has value 17 and it has 2 children 22 and 15. 15 will be left child and 22 will be right child. If the node “17” has children 22 and 23, then it will have no left child and both will be adjusted on right.
 Here, we can see that all nodes to the left of 38 are less than 38 and all nodes to the right of 38 are greater than 38. Similarly, the same logic holds for all the sub trees. E.g. 13 has two children 10 and 25. 10 is on left of 13 and 25 is on right of 13. Even though, 12 is not directly attached to 13 but it is on left side of 13 because it is less than 13.
How do we make the class of a node of a Binary Search Tree?
Given below is the C++ code of binary search tree.
Here, we can see that all nodes to the left of 38 are less than 38 and all nodes to the right of 38 are greater than 38. Similarly, the same logic holds for all the sub trees. E.g. 13 has two children 10 and 25. 10 is on left of 13 and 25 is on right of 13. Even though, 12 is not directly attached to 13 but it is on left side of 13 because it is less than 13.
How do we make the class of a node of a Binary Search Tree?
Given below is the C++ code of binary search tree.
- struct node
- {
- int info;
- node *left;
- node *right;
- node()
- {
- left=NULL;
- right=NULL;
- }
- };