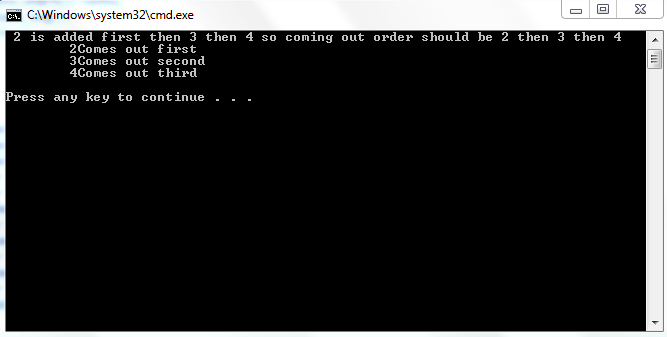
Learning Queues in c++
In this tutorial, you will learn
1. The concept of queues
2. Implementation of queue
3. Array Based implementation of queues
What is the concept behind queues?
Queue is a type of data structures which works on the basis of First In First Out “FIFO”. It means that the data coming first is discharged first. Thus, data is entered from one end and taken out from other end. It is a linear data structure.
Example: To understand, queues better, we can take example of a ticket line. In a line, the person entering first is always served first. Similarly, if a person is making a management system for a bank, the customer who came first is served first.
How can queues be implemented?
Queues can be implemented in a variety of ways but the two most used implementations are:
1. Array Based Implementation
2. Pointer Based (Linked list Based) Implementation.
What is the Array Based Implementation of Queues?
class Queue
{
private:
int arr[10];
int front;
int rear;
public:
Queue():rear(0), front(0)
{}
void enQueue(int value)
{
if((rear+1)%10==front)
{
cout<<"\nQueue is Full\t";
return ;
}
rear=(rear+1)%10;
arr[rear]=value;
}
bool isEmpty()
{
return (front==rear);
}
int deQueue ()
{
if(isEmpty())
{
cout<<"\nQueue is Empty\t";
return 0;
}
front=++front%10;
return arr[front];
}
};
Given above is the C++ object oriented Array Based Implementation of queues. Just as in case of stacks, array based implementation is used when we have an idea of maximum number of data that can be entered in a data structure. If we don’t know the maximum number of data, we can make a very large array but this would waste a lot of space. The edge of Array Based Implementation over Linked List Based Implementation is that in arrays, each element occupies unit space where as in linked list, each data element has unit space for itself and additional space for a pointer. On the other hand, Linked List Based implementation is dynamic. The implantation one wants to use depends on the application.
For Array Based Implementation, an array is made where data will be stored. We have made array of size 10 to explain the concept. The array based implementation of queues is a bit tricky but very easy if you grasp it. Apart from array, two other integers are made. One is rear ad one is front. There is use of both these integers. The use of these integers will be clear once we go through the functions.
In constructor, both integers i.e. front and rear are given value equal to zero. This is important because it will be used to implement the concept of FIFO “First In First Out” We have to make use of these integers. In FIFO, the data is not inserted and removed from same end. And if we remove a data from start of array, either we have to let that space wasted or shift all data back one by one which requires a lot of resources.
Enqueue function is used to insert data in queue. If (rear+1)%10 is equal to front then the queue is full. Actually when we insert data, we increase rear and when we remove data, we increase front. So queue can be thought of as circular. And if rear comes behind front it means that queue is full. After checking if the queue is full or not. We insert data. We simply increment insert data and increment rear.
Then, the next function is to check empty. It is very clear that if rear equals front, then the data structure is empty. Even in constructor, rear and front are given equal value that indicates that the data structure is empty. If at some other stage, after some deletions and insertions, rear becomes equal to front then it indicates that queue is empty.
The last function is deque (deletion) . We first check whether the queue is empty or not. If the queue is not empty, then we increment front and return the element. The element is not deleted in literal sense. When front is incremented, according to the logic of code, that place will be available for next data to be over written.
Note: In next tutorial, Linked List Based Implementation of queues will be discussed and queues will be wrapped.
Output: