Trees in C++ Final part
In this tutorial, you will learn
1. Different types of traversal of BST
2. Concept and implementation of inorder traversal
3. Concept and implementation of preorder traversal
4. Concept and implementation of postorder traversal
What are different types of traversals of BST?
In trees, there are three types of traversals
1. In-order traversal
2. Post-order traversal
3. Pre-order traversal
What is in-order traversal?
In inorder traversal, first the left child is accessed then root and then right child at last. Note, that when we access left child, it may act as a root to another tree and we before accessing it, we must access its left child first.
To explain the traversal further, I will use a picture to help me in explaining.
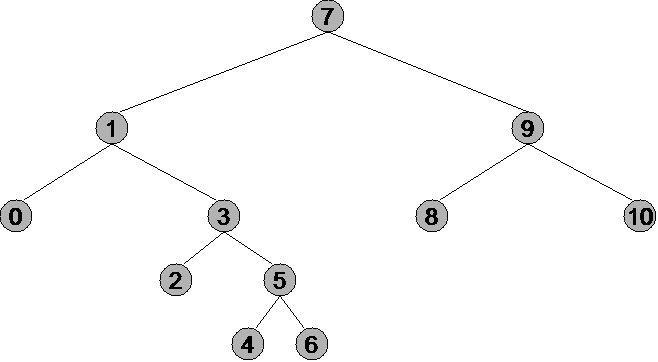
The inorder traversal of this tree would be 0,1,2,3,4,5,6,7,8,9,10. The most important thing about inorder traversal is that if we call inorder traversal on a Binary Search Tree then the result would be in ascending order. The C++ implementation is given below.
void Inorder(node * root)
{
if (root!=NULL) {
Inorder(root->left);
cout<<root->info;
Inorder(root->right);
}
}
As, we know that in inorder traversal, first we start from node on left of root ( say X) and then if X has further nodes at its left then we first access that and so on we continue. Hence, recursive solution would be better in this case. In above case, we continuously check whether we have reached NULL or not. When we are at NULL then we return back one step and reach leaf and we start from leaf and then continue so on. We are calling inorder on left root and then right root. As this is an iterative solution, so we must remember that when we enter Inorder(root->left) we keep digging in and we come back to root and then right once at some level lefts end.
Dry run:
We start from left of root which is 1 and call the inorder again and then we go to left of 1 which is 0 and then left of 0 which is NULL and then we come back to 0 which is printed and then go back to 1 and then we go to 3. Instead of printing 3, we go to left of 3 which is 2 and then after going to NULL, we return to 2 and print it and then we return to 3 and print it and then we go to 5. First we go to its left and get 4 printed then 5 itself and then its right one which is 6. Then, we return to the root of Binary Search Tree which is 7 and then to right of 7and then the same process occurs in right of root.
What is preorder traversal?
In preorder traversal, we first visit the root and then the left sub tree and at last the right sub tree. For the tree given in part of in-order, the result of pre order traversal would be
7,1,0,3,2,5,4,6,9,8,10
The code of preorder is given below
void Preorder(node * root)
{
if (root!=NULL) {
cout<<root->info;
Preorder(root->left);
Preorder(root->right); }
}
This is clear in the code than at any level, first we access root and then left sub tree and then the right sub tree. I state again that it is due to recursive nature of code that it is difficult to understand. Dry run of inorder traversal is given and I would advise you to go through it for complete understanding.
What is postorder traversal?
In post order traversal, we first access the left sub tree and then the right sub tree and then the root. While accessing any of the sub tree, the same steps are carried that first its left sub tree is accessed then the right one and then the root.
void Postorder(node * root)
{
if (root!=NULL) {
Postorder(root->left);
Postorder(root->right);
cout<<root->info;}
}
It is clear from code that the left sub tree is accessed first and then the right sub tree and then the root. Do go through the dry run of inorder traversal and then try to dry run postorder traversal.
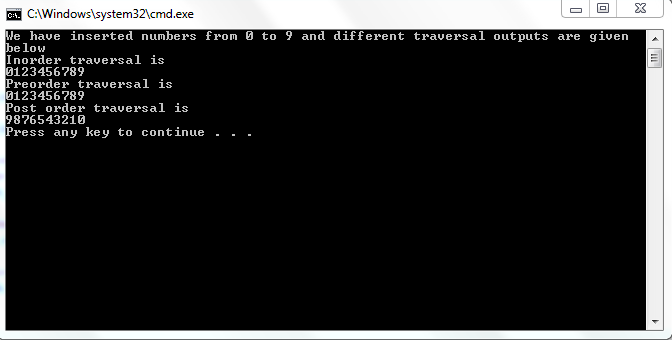
Output:
