Binary Search Tree in C++
Note: We will use BST as abbreviation for binary search trees. Code is given with the tutorial separately for thorough understanding.
In this tutorial, you will learn
1. About the data members of class of BST.
2. Implementation of constructor of BST.
3. Implementation of function to check whether BST is empty.
4. Implementation of function to insert a node in BST.
What are the data members of BST?
The class of Binary search tree has only one data member which is a pointer to the node of BST. It is named as root. If you recall that root is the top most node, you will understand that we make a pointer pointing to the top most node and if we can access top most node, we can access the entire tree as each node has the information of nodes after that.
What is the implementation of constructor of BST?
The implementation of constructor of BST is
tree()
{
root=NULL;
}
<c>
In the constructor of BST, we just give “NULL “ value to root which is a pointer to node. This NULL value is later on used to know whether the BST is empty or not. It is also used during traversal to know when we reach the end of BST or when we reach a leaf node.
<strong>What is Implementation of function to check whether BST is empty?</strong>
<c>
bool isempty()
{
if(root==NULL)
{
return 1;
}
else
{
return 0;
}
}
As we know, in the constructor of BST tree, the value given to root is NULL. So, if root is equal to NULL, there is no node in BST and if root is not equal to NULL then there are nodes in BST. Also while inserting a node, root’s value is adjusted so that it points to the top most node of BST.
What is the implementation of function to insert a node in BST?
Given below is a function to insert a node in BST.
void insert(int value)
{
node* Tnode;
node *cur;
cur=root;
Tnode=new node;
Tnode->info=value;
if(root==NULL)
{
root=Tnode;
}
else
{
while(cur!=NULL)
{
if(cur->info>value)
{
if(cur->left==NULL)
{
cur->left=Tnode;
}
else cur=cur->left;
}
else if(cur->info<value)
{
if(cur->right==NULL)
{
cur->right=Tnode;
}
else cur=cur->right;
}
else return;
}
}
}
};
First of all, the argument is an integer. When you want to add a node, basically you want to add data and this integer is the data you want to add. We make two pointers to a node. First one is named as curr as second one is named as Tnode. We make current point to root which is the top most node and make a new node and make Tnode point to that. First of all, we check whether the BST is empty or not. If it is empty, we simply make root point to new node. If it is not empty then we check whether the data to be inserted is either less than or greater than the value of root node. The next step is easy once you grasp the concept. A loop is created which goes until we reach a leaf. Data is inerted only at the leaf. The while loop continues until curr points to NULL. When we want to add some number, we check whether this number is smaller than or greater than the number curr is pointing to. If it is less, we proceed to left child and if it is greater, we proceed to right child. This process continues until we reach a leaf node and insert the data next to it. We check whether we have reached a leaf node or not during every iteration of while loop. Thus, when we insert a data this way, it always becomes a leaf. In case you have forgotten what a leaf is, leaf is the node which has no further children. Just to dry run, if the BST has a single node root, the first condition will be false and we will come to else and enter while loop. If the data is less than the root, it will be put in left of root, other wise in the right of root.
Note: In next tutorial, some other functions of BST will be discussed.
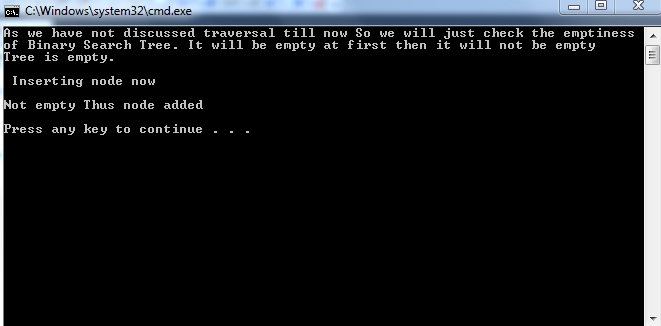
Output: