2 Dimensional Arrays
In this part you will learn:
1. C syntax
2. 2D arrays
3. Nested for loops
4. Showing output
In this tutorial I will teach you about 2D arrays. 2D arrays can be called array of arrays. First we had a single array that was in just one single dimension and we accessed its elements by writing the index in the subscript. In 2d arrays we have arrays that go in both direction. So now we access its elements by mentioning the row number as well as the column number in the subscript separately.
Matrix Operation
Basic Step:
Open Dev C++ then File > new > source file and start writing the code below.
#include<stdio.h>
#include<conio.h>
These two are the most common and basic header files. The first one stdio.h is used to grant us most of the basic functions of C like Input and Output functions. The second one conio.h provides us functions like getch() which is used to pause our screen until we press a button.
int main()
{
int matrix[100][100];
int rows,columns;
printf("Enter the number of rows:");
printf("Enter the number of columns:");
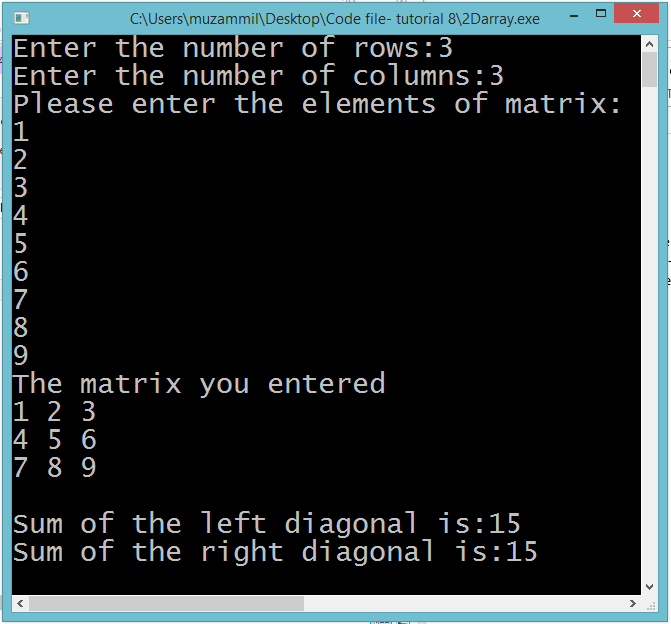
printf("Please enter the elements of matrix:\n");
int i,j;
for( i=0;i<rows;i++)
{
for( j=0;j<columns;j++)
{
scanf("%d",&matrix
[i
][j
]); }
}
In this program we declared a 2d array of integers. We will treat it like a matrix in mathematics. This is because the concept of 2d arrays can be very well understood by with the implementation of matrixes. We will calculate the sum of diagonals of matrix separately in this program.
At first we declared a 2d array of integers with 100 rows and 100 columns. The first number in the subscript is always the number of rows of the matrix and the second in the subscript is the total column number. Then we took input from the user the number of rows and columns. This is because we want the user to tell us how big he wants to build a matrix.
For this program the user should enter same number of rows and columns because the diagonal sum can only be calculated of square matrix. Then we wrote a nested for loop to take input the elements of the matrix.
The first for loop is to shift the rows of the matrix and the second or the inner for loop is to iterate between the columns of the matrix. For every row of the matrix the inner for loop runs column times so we can enter the value of each element of the matrix.
printf("The matrix you entered\n"); int k,l;
for( k=0;k<rows;k++)
{
for( l=0;l<columns;l++)
{
}
}
Now after taking input all the elements of the matrix we are printing them using the similar nested for loops but this time we are printing the value of the elements columnwise.
int sum=0,m;
for(m=0;m<rows;m++)
{
sum=sum+matrix[m][m];
}
printf("\nSum of the left diagonal is:%d",sum
);
In this for loop we are calculating the sum of the principal diagonal or the left diagonal of matrix. What we are doing is we are running a single for loop that is adding all the elements of the matrix with same row and column number. Then after the loop we are printing the value of the sum of the diagonal.
j=columns-1;
sum=0;
for(m=0;m<rows && j>=0;m++,j--)
{
sum=sum+matrix[m][j];
}
printf("\nSum of the right diagonal is:%d",sum
);
}
In this part we are calculating the sum of the right diagonal of the matrix. For this we have to increase the row number while decreasing the column number. For this we initialized a variable j with column -1 so that it becomes the last index of the column. The rest of the program is same. We accumulated the sum in a single variable called sum and then at the end we printed the value.
Execute > compile
then Execute > run
Output